动态规划之背包问题

前面介绍了一些最常见的动态规划题型和对应解法，而实际上，动态规划最经典的题型非背包问题莫属，并且大多数人最初都是从背包问题入坑进而打开动态规划这一大门。

背包问题分为多种，其中最常见的主要是三类：01背包、完全背包、多重背包。这里面最经典的是01背包问题，它基本上已经成为了事实上的动态规划入门级必学算法。下面，我们将对上述的三类背包问题逐个分析。

---

01背包问题

问题描述

有一个容量为 $V$ 的背包，和 $n$ 件物品。这些物品分别有两个属性：体积 $w$ 和价值 $v$，且每种物品都只有一个。现要求将这些物品在不超过容量 $V$ 的前提下装入背包中，并使得此背包的价值最大。问该最大值是多少？

注：由于在该问题的所有解中，每个物品只有两种可能的情况：在背包中、不在背包中（即背包中的任意物品数量只能为 0 或 1），因此该问题被称为 0-1 背包问题。

算法分析

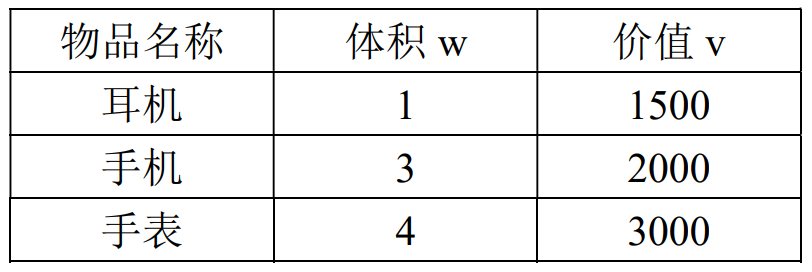
为理解此问题的实质，下面我用一个实际例子来进行讲解。假设现在有以下 3 件物品，以及一个容量为 4 的背包，现在你想知道，你的背包所能装下的最大价值是多少。

最简单的办法，我们可以将这3件物品的所有组合枚举出来，然后求出每种组合的价值，最终输出最大值即可。高中时大家都学过集合，我们知道，对于某个具有 $n$ 个元素的集合 $\Phi$，其子集个数为 $2^n$。也就是说对于有 $n$ 件物品的集合，其可能的组合方案有 $2^n$ 个。比如对于上面这 3 件物品，其可能的组合就有 $2^3=8$ 个，如下

接下来我们将其中满足总容量不大于 4 的组合方案选出，并将其作为一种合法的选取，于是可以得到此类方案对应的总价值集合：{ 0，1500，2000，3000，3500 }，最终取出其中的最大值 3500 即可（经验证，此为正确答案，即选择组合{ 耳机，手机 }）。

这样的算法很容易理解，但是弊端非常大：严重耗时。比如当待选物品有 100 件时，此时总的组合方案数将达到 $2^{1}00$ 个，要枚举这所有的组合必然超时。而实际上，对于100件物品而言，这个数据范围却并不大，所以上面的枚举法是行不通的。

前面说了，动态规划算法的基本思想是将待求解问题分解成若干个子问题，然后再将这些子问题分阶段处理以避免重复计算来进行求解的。这里面最关键的一步，在于寻找问题的动态转移方程（即递推式）。接下来，我们依然通过填表来寻找这一规律，先将背包问题的网格绘出，如下：

其中每个格子的含义为（假设当前为第 $i$ 行、第 $j$ 列）：在当前背包容量为 $j$、可选第 $i$ 行及其之前的所有物品（按序排列）的前提下，能够选到的最大价值。

接下来我们需要填充其中的每个单元格，当网格填到最后一行最后一列时，即求到了在容量为 $V$、可选所有商品的条件下背包所能容纳的最大价值。

首先是第一行（可选耳机），我们需要尝试把耳机装入背包以使背包的价值最大。在每个单元格，都需要做一个简单的决定：要不要耳机？别忘了，你要找出一个价值最高的商品集合。第一个单元格表示背包的容量为1，耳机的体积也是1，这意味着它能装入背包！因此，这个单元格包含耳机，价值为 1500。于是可以填充网格，如下图所示：

与第一个单元格相同，每个单元格都将包含当前可装入背包的所有商品。来看下一个单元格，这个单元格表示背包的容量为 2，完全能够装下耳机！

这行的其他单元格也一样。别忘了，这是第一行，只有耳机可供你选择。换言之，你假装现在还没法拿其他两件商品。于是我们接着完善第一行的剩余单元格，最终的结果如下图所示：

此时，整个第一行表示的是在背包容量为 4、可选耳机时，可在其中装入的商品的最大价值为 1500。
现在你很可能心存疑惑：原来的问题说的是容量为4的背包，我们为何要考虑容量为 1、2、3 的背包呢？前面说过，动态规划是从小问题着手，逐步解决大问题。这里解决的子问题将帮助后面我们解决大问题。其实这正是体现动态转移的一个方面。

当然，现在得到的解并不是最终的，随着程序的执行（表格的填写），我们将逐步修改最大值。
接下来填充第二行（可选耳机、手表）。我们先看第一个单元格，它表示容量为 1 的背包。在此之前，可装入容量为1的背包的商品最大价值为 1500。现在面临一个新问题：该不该拿手表呢？当前背包的容量为 1，能装下手表吗？太大了，装不下！由于容量 1 的背包装不下手表，因此最大价值依然是 1500，如下：

接下来两个单元格的情况与此相同。在这些单元格中，背包的容量分别为 2 和 3，由于这些背包都装不下手表，而以前的最大价值为 1500，因此最大价值保持不变。于是得到表格如下：

背包容量为 4 呢？终于能够装下手表了！原来的最大价值为 1500，但如果在背包中装入手表而不是耳机，那么总价值将变为 3000！因此还是拿手表吧。于是更新表格如下：

下面用同样的方法填写最后一行。由于手机体积为 3，无法将其装入容量为 1 或 2 的背包中，因此前两个单元格中的最大价值依然是 1500，如下：

对于容量为 3 的背包，原来的最大价值为 1500，但现在你可选择拿价值 2000 的手机而不是耳机，这样新的最大价值将变为 2000！于是更新表格如下：

对于容量为 4 的背包，当前最大价值为 3000，但你可以选择不拿手表，而拿手机。虽然它只值 2000，价值没有原来高，但手表的体积只有 3，背包还剩下 1 的容量没用！在 1 的容量中，可装入的商品的最大价值是多少呢？你之前计算过，是价值为 1500 的耳机，此时 2000+1500 > 3000，于是可直接更新表格为：

最终，在上面填写的表的最后一个单元格里（即最后一行最后一列所在位置）就存放着该背包所能装下的最大价值。

注：在计算最后一个单元格的最大价值时，我们选择拿手机，此时还剩下1的容量，于是我们直接加上该行单元格中的第一个单元格内容（即 2000+1500）便得到了这种方案下的总价值，最后再与之前的总价值（即 3000）比较大小，并将较大者写入其中。这一操作，实际上就体现了动态转移的思想（以递推的方式取代递归求解）。

也许你会认为我在计算最后一个单元格的价值时，使用了不同的公式。那是因为填充之前的单元格时，我故意避开了一些复杂的因素。其实，计算每个单元格的价值时，使用的公式都相同。如下：

$$\begin{array}{rl}dp[i][j]& =max(上方单元格的价值，剩余空间的价值+当前商品的价值)\\ & =max(dp[i-1][j]，dp[i-1][j-当前商品的体积]+当前商品的价值)\\ & =max(dp[i-1][j]，dp[i-1][j-w[i]]+v[i])\end{array}$$

其中，$dp[i][j]$ 表示表格中的第 $i$ 行第 $j$ 列单元格中的值。下面我们用一道实际的题目来趁热打铁，并进一步分析如何将二维状态转移方程优化至一维。

---

洛谷 P1048 采药

问题描述

辰辰是个天资聪颖的孩子，他的梦想是成为世界上最伟大的医师。为此，他想拜附近最有威望的医师为师。医师为了判断他的资质，给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说：“孩子，这个山洞里有一些不同的草药，采每一株都需要一些时间，每一株也有它自身的价值。我会给你一段时间，在这段时间里，你可以采到一些草药。如果你是一个聪明的孩子，你应该可以让采到的草药的总价值最大。”
如果你是辰辰，你能完成这个任务吗？

输入格式

第一行有 2 个整数 $T(1\le T\le 1000)和M(1\le M\le 100)$，用一个空格隔开，$T$ 代表总共能够用来采药的时间，$M$ 代表山洞里的草药的数目。

接下来的 $M$ 行每行包括两个在 1 到 100 之间（包括 1 和 100）的整数，分别表示采摘某株草药的时间和这株草药的价值。

输出格式

1 个整数，表示在规定的时间内可以采到的草药的最大总价值。

样例输入

70 3
71 100
69 1
1 2

样例输出

3

算法分析

对于某株草药而言，采集与否只有两种情况，因此属于01背包问题。实际上，本题中的采药总时间 $T$ 就相当于01背包问题中的背包容量 $V$、某株草药的采摘时间及其价值则对应01背包问题中某种商品的体积和价值。因此，根据前面对01背包问题的分析和状态转移方程可以直接写出如下代码：

#include<iostream>
using namespace std;

const int N=1005;
const int M=105;
int n,m;
int dp[M][N],t[M],v[M];

int main()
{
	cin>>n>>m;
	for(int i=1;i<=m;i++) cin>>t[i]>>v[i];
	for(int i=1;i<=m;i++)
		for(int j=1;j<=n;j++)
			if(j>=t[i])
				dp[i][j]=max(dp[i-1][j],dp[i-1][j-t[i]]+v[i]);
			else
				dp[i][j]=dp[i-1][j];
	cout<<dp[m][n]<<endl;
	return 0;
}

上述代码是一个满分代码，但是不够完美。因为此算法存在一个显著缺陷：$dp[M][N]$ 数组在 $M$或 $N$ 取值较大时可能会出现爆内存的现象。因此，我们需要设法进行降维。从哪儿降呢？要么变成$dp[M]$，要么变成 $dp[N]$。如果是保留 $dp[M]$，这意味着在进行状态转移时，是以草药的种类来进行的（即在二维表格中填表时按列进行），这和前面我们采取的填表方式相悖；而如果是保留 $dp[N]$，那么我们在进行状态转移时就是以背包容量来进行的（即在二维表格中填表时按行进行），这和前面采取的填表方式一致。这就提示我们，可以将药的种类省略，而仅用一个和背包容量相当的一位数组 $dp[N]$ 来进行状态转移。此时，我们可以利用一个循环，来将输入的数据不断与前面的数据进行计算、比较，并将最新结果保存至 $dp[N]$中。据此，可以得到新的递推式为：

$$dp[j]=\text{max}(dp[j],dp[j-w[i]]+v[i])$$

但是这里有个新问题，当在一维数组中从左至右更新 $dp[N]$ 数组时，由于 $dp[j-w[i]]+v[i]$ 总是大于 $dp[j]$，因此这将使得某个物品被反复拿多次。以上面的例子举例（在以下物品中拿最大价值，背包总容量为 4）：

那么在利用递推式：

$$dp[j]=\text{max}(dp[j],dp[j-w[i]]+v[i])$$

进行动态转移时，其更新过程如下（注：$dp[N]$ 数组在初始情况下的所单元格中的值均为0）：

• 第一个单元格，此时 $dp[1]=\text{max}(dp[1],dp[1-1]+1500)=\text{max}(0,0+1500)=1500$；
• 第二个单元格，此时 $dp[2]=\text{max}(dp[2],dp[2-1]+1500)=\text{max}(dp[2],dp[1]+1500)=max(0,1500+1500)=3000$；
• 第三个单元格，此时 $dp[3]=\text{max}(dp[3],dp[3-1]+1500)=\text{max}(dp[3],dp[2]+1500)=max(0,3000+1500)=4500$；
• 第四个单元格，此时 $dp[4]=\text{max}(dp[4],dp[4-1]+1500)=\text{max}(dp[4],dp[3]+1500)=max(0,4500+1500)=6000$；
  ……

可以发现，从第 2 个单元格开始，后面将一直错下去，因为这之后的每次更新都会利用前面的计算结果（实际上，这样的执行流程在逻辑上表示重复取当前物品，即某件物品不再是被拿了一次，而是被拿了多次）。

注意：这里的 “错误” 做法，洽洽又是后面完全背包问题的正确处理办法。

这又该如何处理呢？我们来分析出现这种情况的原因。由于大容量的背包在存放物品时可能不仅能存放前面已经存放的，或许还会因为大容量而使得其能拿更多的物品，从而出现反复拿小体积物品的情况。因此在自左向右更新的过程中，由于取 $\text{max}(dp[j],dp[j-w[i]]+v[i])$ 而使得后面的数组在更新时不断利用前面已经保留好的结果来进行状态转转移，进而不断出错（即对某件物品反复拿取）。

虽然如此，但这个递推公式本身是正确的，只是在使用过程中由于更新方向而出现了一些错误。试想，如果从右向左对数组进行更新是否可行呢？在这种情况下，当用到：

$$dp[j]=\text{max}(dp[j],dp[j-w[i]]+v[i])$$

时，由于 $dp[j-w[i]]$ 指向的数组还未进行更新，此时其存放的结果是在前一种情况下（只能拿前一种及其更之前的物品时），对应容量背包所能存放的最大价值。故此时 $\text{max}(dp[j],dp[j-w[i]]+v[i])$ 表示的含义正是：“在当前背包容量下，怎样的拿取方案具有更大价值：延续上一种拿取方案 or 拿当前物品再加上除开当前物品体积后剩余背包容量所具有的最大价值后的总价值”。这和我们所期望的效果是一致的。下面给出改进后（降维使用滚动数组）的完整代码：

#include<iostream>
using namespace std;

const int N=1005;
const int M=105;
int n,m;
int dp[N],t[M],v[M];

int main()
{
	cin>>n>>m;
	for(int i=1;i<=m;i++) cin>>t[i]>>v[i];
	for(int i=1;i<=m;i++)
		for(int j=n;j>=t[i];j--) // 在 j < t[i] 的这部分（dp[j]），dp[] 数组将延续之前的状态，因此不用更新
			dp[j]=max(dp[j],dp[j-t[i]]+v[i]);
	cout<<dp[n]<<endl;
	return 0;
}

---

完全背包问题

问题描述

有一个容积为 $V$ 的背包，同时有 $n$ 种物品，每种物品均有各自的体积 $w$ 和价值 $v$，每种物品的数量均为无限个，求使用该背包最多能装的物品价值总和。

算法分析

实际上，完全背包问题就是在01背包问题的基础上，将每种物品的数量由 1 个变为无限个。因此，完全背包问题中的递推式也将随之发生改变。在01背包问题中，其递推式为：

$$dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i])$$

基于以上公式在填表的第一行时，其结果如下：

可以看出，在填写第一行的第 2、3、4 列时，尽管背包容量增加了，但是由于耳机只有一个，所以后面背包的最大值一直未发生变化，其取值始终为一个耳机的价值。但是现在的情况有所不同，我们可以在不超过背包容量的前提下，多拿几个耳机。此时，填表的结果应该如下：

基于此，我们可以很自然地想到在01背包问题的算法中，于最内层再加一重循环，这层循环用于确定当前单元格（即 $dp[i][j]$）到底取多少个物品会使得当前价值最大（但不能超过背包容量）。于是此时的状态转移方程就变成了（其中，$k$ 表示当前物品拿了多少个）：

$$dp[i][j]=max(dp[i-1][j],dp[i-1][j-k\ast w[i]]+k\ast v[i])$$

这便是完全背包问题中最关键的递推式了，下面我们同样以一个实际例题来练练手

---

洛谷 P1616 疯狂的采药

问题描述

辰辰是个天资聪颖的孩子，他的梦想是成为世界上最伟大的医师。为此，他想拜附近最有威望的医师为师。医师为了判断他的资质，给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说：“孩子，这个山洞里有一些不同种类的草药，采每一种都需要一些时间，每一种也有它自身的价值。我会给你一段时间，在这段时间里，你可以采到一些草药。如果你是一个聪明的孩子，你应该可以让采到的草药的总价值最大。”
如果你是辰辰，你能完成这个任务吗？
此题和原题（P1048 采药）的不同点：

1. 每种草药可以无限制地疯狂采摘。
2. 药的种类眼花缭乱，采药时间好长好长啊！（暗示数据范围更大）

输入格式

输入第一行有两个整数 $T（1\le T\le 100000）$ 和 $M（1\le M\le 10000）$，用一个空格隔开，$T$ 代表总共能够用来采药的时间，$M$ 代表山洞里的草药的数目。接下来的M行每行包括两个在 1 到 10000之间（包括 1 和 10000）的整数，分别表示采摘某种草药的时间和这种草药的价值。

输出格式

输出一行，这一行只包含一个整数，表示在规定的时间内，可以采到的草药的最大总价值。

样例输入

70 3
71 100
69 1
1 2

样例输出

140

算法分析

根据前面对完全背包的分析，我们可以直接写出以下代码：

#include<iostream>
using namespace std;

const int N=1005;
const int M=105;
int n,m,maxValue,temp;
int dp[M][N],t[M],v[M];

int main()
{
	cin>>n>>m;
	for(int i=1;i<=m;i++) cin>>t[i]>>v[i];
	for(int i=1;i<=m;i++)
		for(int j=1;j<=n;j++){
			maxValue=0;
			for(int k=0;k*t[i]<=j;k++){
				temp=dp[i-1][j-k*t[i]]+k*v[i];
				if(temp>maxValue) maxValue=temp;
			}
			dp[i][j]=maxValue;
		}
	cout<<dp[m][n]<<endl;
	return 0;
}

题目的数据范围是很大的，如果真的令 $N=100000,M=10000$，那么对于 $dp[N][M]$，连编译都通不过。于是为了能骗取部分分，就写了以上代码，从逻辑上该代码的思路是完全正确的，比如对于测试数据：

10 4
7 9
4 5
3 3
2 1

正确的输出为 12，得到的 $dp[]$ 矩阵如下：

$$\left[\begin{array}{cccccccccc}0& 0& 0& 0& 0& 0& 9& 9& 9& 9\\ 0& 0& 0& 5& 5& 5& 9& 10& 10& 10\\ 0& 0& 3& 5& 5& 6& 9& 10& 10& 12\\ 0& 1& 3& 5& 5& 6& 9& 10& 10& 12\end{array}\right]$$

因此上述代码确实解决了完全背包问题，但是新问题也随之引出：

1. 程序中使用了二维数组，在数据范围过大的情况下连编译都过不了；
2. 程序中使用了三重循环，在数据范围稍大的情况下会超时。

接下来我们就着手对上面的问题进行优化。首先是降维，那就需要把状态转移方程变为：

$$dp[j]=\text{max}(dp[j],dp[j-k\ast w[i]]+k\ast v[i])$$

维度是降低了，但是如何更新呢？此时，突然想起一件事！！！在前面 01 背包问题中我们讨论降维时，出现了一个有趣的现象——如果更新 $dp[]$ 数组时采用自左向右的方向，那么在后面进行更新时，其执行逻辑是“可重复拿取某件物品”！巧了，现在我们所作的假设就是所有物品都有无数件（即可重复拿），这不正好就可以拿来用了么？换言之，现在我们不再需要用最里面的那层 $k$ 循环来确定某个网格到底拿多少物品才能使得背包总价值最大，而是通过采取和 01 背包问题中相反的更新 $dp[]$ 数组方向来实现。这样一来，我们还顺带解决了时间复杂度过高的问题！

实际上，采用从左到右的方式更新 $dp[]$ 数组时，相当于是在遍历每个容量的背包时，判断当前背包是否能装下任意物品，只要能装下，那就装！这是一种贪心的思想，它恰好符合完全背包的题境。

下面给出经过优化后的完整满分代码：

#include<iostream>
using namespace std;

const int N=100005;
const int M=10005;
int n,m;
int dp[N],t[M],v[M];

int main()
{
	cin>>n>>m;
	for(int i=1;i<=m;i++) 
		cin>>t[i]>>v[i];
	for(int i=1;i<=m;i++)
		for(int j=t[i];j<=n;j++)
			dp[j]=max(dp[j],dp[j-t[i]]+v[i]);
	cout<<dp[n]<<endl;
	return 0;
}

多重背包问题

问题描述

有容积为 $V$ 的背包，给定一些物品，每种物品包含体积 $w$、价值 $v$、和数量 $k$，求用该背包能装下的最大价值总量。

算法分析

01 背包问题与完全背包问题实际上是两种极端，而多重背包问题则正是介于这两者之间的一种情况。基于此，我们可以将多重背包问题转化为 01 背包或完全背包问题来进行求解。

1. 可以把某种物品中的 $k$ 个视为 $k$ 种不同物品，此时再对所有物品按照01背包问题来进行处理。这样的转化当然是成立的，但是仅在数据范围较小时才适用，一旦每种物品的数量稍大一点，在时间上必然有超时的风险。此时，对于某种物品（假设有 $k$ 个），若我们采用一种更精炼的划分方案，就会使得该物品分类下来的组数大大减少。比如可以采用二进制的拆分将原来的 $k$个物品分为： { 1 , 2 , 4 , … , k − 2 i + 1 } \{1, 2, 4, \dots, k-2^i+1\} {1,2,4,…,k−2i+1} 这些组，以替代最初的分类： { 1 , 1 , 1 , … , 1 } \{1,1,1,\dots,1\} {1,1,1,…,1} 这些组，这是一个 ${\text{log}}_2(n)$级别的数量优化。
2. 若存在某个物品，其数量 $k$ 乘以其单位体积大于背包总容量（即 $k\ast w[i]>V$），那么此时对于该物品而言，它与背包之间是完全背包问题。

上述两点分别从 01 背包和完全背包的角度对多重背包问题进行了转化，而多重背包正好也是介于 01 背包和完全背包之间的问题。正是这两点，使得我们能设计出一个可以与 “单调队列优化” 分庭抗衡的算法。下面还是用一个实际例题来练手，以巩固理解。

---

超市里的狂欢夜

问题描述

辰辰参加的非常 6+1 的节目已经走到最后一关啦！这一关的游戏规则如下：

每个参赛者都会被派发一个推车，这个推车只能承受质量为 $n$ 的重量，参赛者可以用这个推车在超市里拿取任意数量的商品。当然，不同商品的重量、价格以及数量都是不同的。在游戏开始时，每个参赛者都会被派发到不同的超市中，在经过规定时间后，参赛者的推车中商品价值最高的人获胜，并且他将获得推车中的所有东西。

辰辰通过查阅该超市中的商品信息，得到了所有商品的重量、价格与数量信息。

你能根据这些信息帮辰辰找出他能够取到的最大价值么？

输入格式

输入的第一行有两个整数 $n（1\le n\le 100000）$和 $m（1\le m\le 10000）$，用一个空格隔开，$n$ 表示推车所能程受的最大重量，$m$ 代表超市中的商品种类数。
接下来有 $m$ 行，每行包括 3 个在 1 到 1000 之间（包括 1 和 1000）的整数，分别表示当前某个商品的重量、价格以及库存数量。

输出格式

输出一行，这一行只包含一个整数，表示辰辰所能取到的最大价值。

样例输入

50 4
10 200 4
15 250 3
20 350 2
25 500 1

样例输出

950

算法分析

根据前面的推理，可分别用 01 背包和完全背包来部分取代多重背包，下面直接给出本题的完整代码：

#include<iostream>
using namespace std;

const int N=100005;
const int M=10005;
int n,m;
int dp[N],w[M],v[M],num[M];

void ZeroOnePack(int weight,int value)				//01背包模型 
{
	for(int i=n;i>=weight;i--)
		dp[i]=max(dp[i],dp[i-weight]+value);
}
void CompletePack(int weight,int value)				//完全背包模型 
{
	for(int i=weight;i<=n;i++)
		dp[i]=max(dp[i],dp[i-weight]+value);
}
void MultiplePack(int weight,int value,int number)	//多重背包模型 
{
	if(number*weight>n){					//如果总容量比这个物品的容量要小，那就退化为完全背包 
		CompletePack(weight,value);
		return;
	}else{									//否则就将其转化为01背包（并利用二进制的拆分来优化） 
		int k=1;
		while(k<=number){
			ZeroOnePack(k*weight,k*value);
			number -= k;
			k<<1;
		}
		if(number!=0) ZeroOnePack(number*weight,number*value);
	}
}

int main()
{
	cin>>n>>m;
	for(int i=1;i<=m;i++) 
		cin>>w[i]>>v[i]>>num[i];
	for(int i=1;i<=m;i++)
		MultiplePack(w[i],v[i],num[i]);
	cout<<dp[n]<<endl;
	return 0;
}

END

---