目录

一.判断是哈密顿图的“充分条件”：

二.判断“不是”哈密顿图的“充分条件”：

三.其他情况：

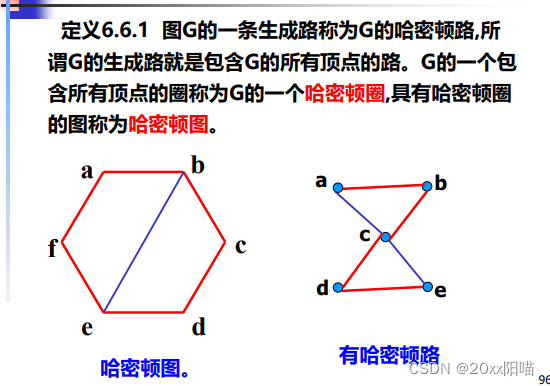
定义：含有哈密顿圈的图称为哈密顿图。补充：哈密顿路即包含所有顶点且不重复的路。（两个对顶三角含有哈密顿路，但不是哈密顿图因为没有哈密顿圈）

一.判断是哈密顿图的“充分条件”：

1.美国图论数学家奥勒在1960年给出了一个图是哈密尔顿图的充分条件：对于顶点个数大于2的图，如果图中任意两点度的和大于或等于顶点总数，那这个图一定是哈密顿图。但不满足不一定就不是哈密顿图
2.若图的最小度不小于顶点数的一半，则图是哈密顿图；
3.若图中每一对不相邻的顶点的度数之和不小于顶点数，则图是哈密顿图。不满足不一定就不是比如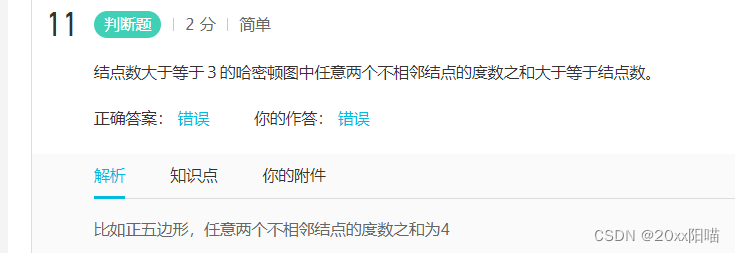

二.判断“不是”哈密顿图的“充分条件”：

1.如果一个图的顶点可以用两种颜色染色，那若结果染完两种颜色的顶点数量不一致，则一定不是哈密顿图；但满足一致，不一定就是哈密顿图。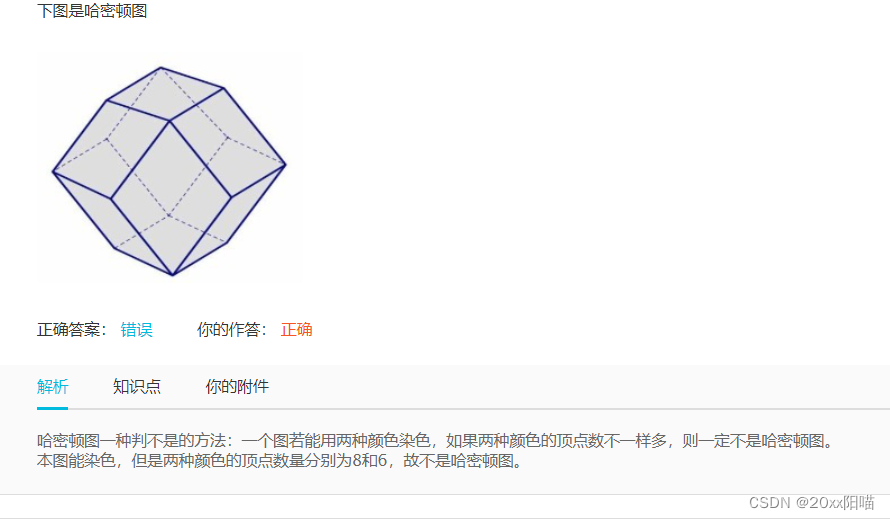

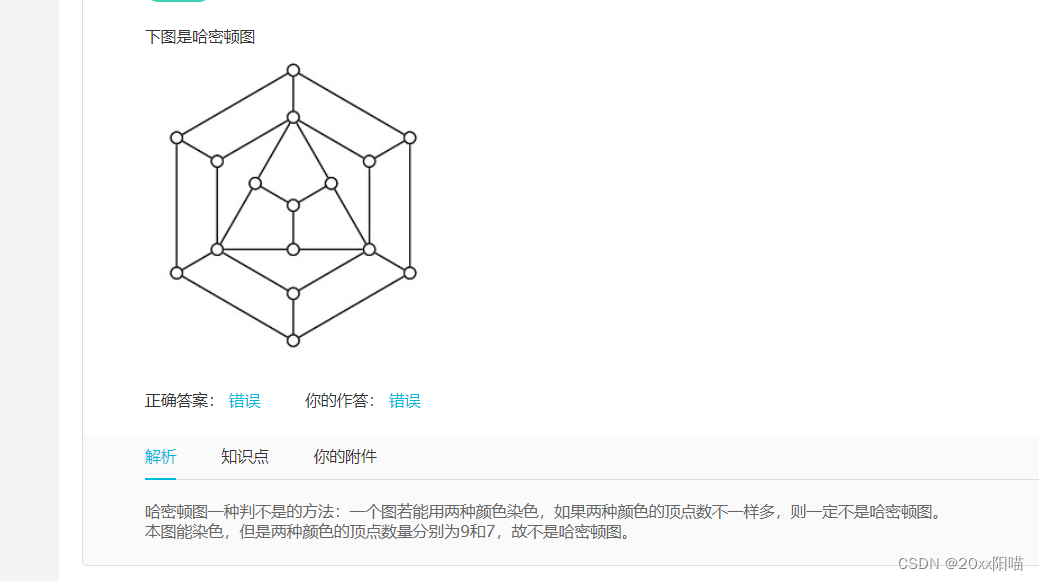
 1’：还有一类是完全偶图，两边顶点各自染成一种颜色，若顶点数不同，即两种颜色数不同，则不是哈密顿图->所以完全偶图是哈密顿图的必要条件是两边的顶点数必须相等

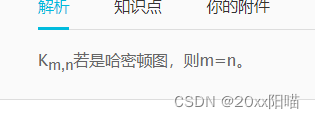
2.（判断是哈密顿图的必要条件）该图去掉s个顶点之后的分支数一定小于等于去掉的顶点数s，若不满足一定不是哈密顿图。

三.其他情况：

1.有三个度数为1的顶点，则必然没有哈密顿路

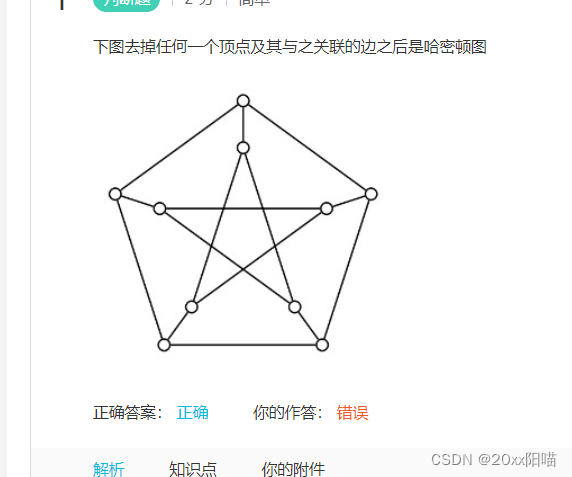
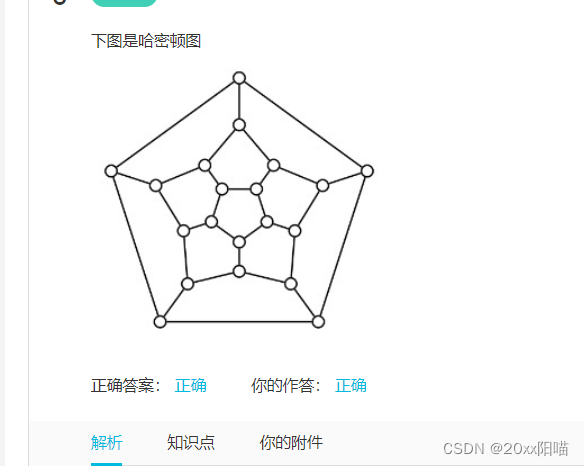
2.有些，自己能用眼和大脑可以想象出那条哈密顿回路

 ps：由于作者学识有限，难免会有些许错误，欢迎大家指正或者补充~