数字逻辑中的反演规则和对偶规则
1、反演规则
若将逻辑函数f表达式中所有的“·”变成“+”,“+”变成“·”,“0”变成“1”,“1”变成“0”,原变量变成反变量,反变量变成原变量,并保持原函数中的运算顺序不变 ,则所得到的新的函数为原函数f的反函数 。这一规则称为反演规则。
。这一规则称为反演规则。
运用反演规则可以很方便地求出一个函数的反函数,但使用反演规则时应注意保持原函数式中运算的优先顺序不变。
2、对偶规则
如果将逻辑函数f表达式中所有的“·”变成“+”,“+”变成“·”,“0”变成“1”,“1”变成“0”,并保持原函数中的运算顺序不变,则所得到的新逻辑表达式称为函数f的对偶式,并记为f’。例如,
注意:求逻辑表达式的对偶式时,同样要保持原函数的运算顺序不变。
若两个逻辑函数表达式f和g相等,则其对偶式f′和g′也相等。这一规则称为对偶规则。根据对偶规则,当已证明某两个逻辑表达式相等时,便可知道它们的对偶式也相等。
3、总结来说,两者的区别在于反演规则除了对0,1取反外,还对变量进行取反;而对偶规则只对0,1取反而不对变量进行取反;
Duality (对偶):FD(X1 , X2 , … , Xn , + , · , ’ )
= F(X1 , X2 , … , Xn , · , + , ’ )
Complement (反演): [ F(X1 , X2 , … , Xn , + , · ) ]’
= F(X1’ , X2’, … , Xn’ , · , + )
[ F(X1 , X2 , … , Xn) ]’ = FD(X1’ , X2’, … , Xn’ )

AtomGit 是由开放原子开源基金会联合 CSDN 等生态伙伴共同推出的新一代开源与人工智能协作平台。平台坚持“开放、中立、公益”的理念,把代码托管、模型共享、数据集托管、智能体开发体验和算力服务整合在一起,为开发者提供从开发、训练到部署的一站式体验。
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容
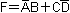


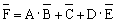










所有评论(0)