K均值(K-means)聚类算法(Python3实现代码)
本文的代码与数据地址已上传至github:https://github.com/helloWorldchn/MachineLearning
一、K-means算法基本思想
1、K-means简介
K-means标准算法是1957 年史都华·劳埃德(Stuart Lloyd)作为一种脉冲码调制的技术所提出,但直到1982年才被贝尔实验室公开出版在《IEEE Transactions on Information Theory》中,原始文献为《Least squares quantization in PCM》(DOI: 10.1109/TIT.1982.1056489)。
术语“k-均值”于1967年才被詹姆斯·麦昆(James MacQueen) 在文献《Some Methods for Classification and Analysis of Multiva》中提出,描述 K-means算法的完整理论并进行了详细的研究。 作为最经典的划分聚类算法,K-means算法的实现并不复杂,具有较高的可伸缩性,同时K-means算法具有良好的可靠性和高效性,是一种广泛应用的聚类算法。
2、K-means算法流程
K-means算法接受一个参数K用以决定结果中簇的数目。算法开始时,要在数据集中随机选择K个数据对象用来当做k个簇的初始中心,而将剩下的各个数据对象就根据他们和每个聚类簇心的距离选择簇心最近的簇分配到其中。然后重新计算各个聚类簇中的所有数据对象的平均值,并将得到的结果作为新的簇心;逐步重复上述的过程直至目标函数收敛为止。
下面介绍该算法的具体步骤:
- 对于给定的一组数据,随机初始化K个聚类中心(簇中心)
- 计算每个数据到簇中心的距离(一般采用欧氏距离),并把该数据归为离它最近的簇。
- 根据得到的簇,重新计算簇中心。
- 对步骤2、步骤3进行迭代直至簇中心不再改变或者小于指定阈值。

K-means算法的流程图
3、K-means伪代码
输入:聚类数目k,数据集
X
=
{
x
1
,
x
2
,
…
x
i
,
…
,
x
n
}
X=\left\{\right.x_1,x_2,…x_i,…,x_n\left\}\right.
X={x1,x2,…xi,…,xn},停止阈值ε,模糊因子m,最大迭代次数T;
输出:聚类中心
C
=
[
c
1
,
c
2
,
…
,
c
k
]
C=[c_1,c _2,…,c_k]
C=[c1,c2,…,ck];
begin
01.C ← Ø, U ← Ø, t ← 0 // 初始化聚类中心C、隶属度矩阵U和迭代次数t
02.while t < T do
03. for i ← 1 to n do
04. for j ← 1 to k do
05. calculate dij //根据公式计算第i个数据和第j个聚类中心的距离
06. if dij = Min{D(Xi ,Zj)} then // 根据距离归类
07. Xi ∈ Cj // 将数据xi归到第j类
08. end for
09. end for
10. for j ← 1 to k do
11. calculate cj //根据公式重新计算聚类中心点
12. end for
13. calculate J //根据公式重新计算目标函数J
14. t += 1
15. if ||J(t) - J(t-1)|| ≤ ε then
16. return C
17. end if
18.end while
19.return C
end
4、K-means时间复杂度分析
在有n个样本的d维数据集X中,数据集被划分成k个簇,如果本次聚类经过了t次迭代,每次迭代需要计算一次目标函数,计算过程中需要分别求出d维数据中k个簇的聚类中心与n个数据的距离,算法在此过程的时间复杂度为O(n∙k∙d)。综上所述K-means算法的时间复杂度为O(n∙k∙t∙d)。但是由于在一般情况下类簇数目k、数据维度d以及算法的迭代次数t均可认为是常量,所以模糊C均值算法的时间复杂度可以简化为O(n)。由此可见,K-means算法的时间复杂度随着数据点的数量增加呈线性增长,同时也受迭代次数、聚类簇数目以及数据维度的影响。
5、K-means优缺点
K-means优点:
- K-means算法收敛速度快,时间复杂度低,计算效率较高;
- K-means算法算法可解释性好,原理简单易于理解;
- K-means算法调参简单,需要调的参数只有聚类簇数K。
K-means缺点:
- K-means算法的参数簇数目(K值)需要手动指定,K值的确定直接影响聚类的结果,通常情况下,K值需要经验和对数据集的理解指定,因此指定的数值未必理想,聚类的结果也就无从保证。
- K-means算法对噪声和异常值敏感,聚类结果容易受到噪声点的影响;
- K-means算法欧氏距离进行相似性度量,适用于簇是凸形或球形的数据集,在非凸形数据集中难以达到良好的聚类效果。;
- K-means算法的初始中心点选取上采用的是随机的方法。K-means算法极为依赖初始中心点的选取:一旦错误地选取了初始中心点,对于后续的聚类过程影响极大,很可能得不到最理想的聚类结果,同时聚类迭代的次数也可能会增加。而随机选取的初始中心点具有很大的不确定性,也直接影响着聚类的效果;
- K-means算法结果不一定是全局最优,只能保证局部最优。
二、K-means实现(Python3)
本文使用的数据集为UCI数据集,分别使用鸢尾花数据集Iris、葡萄酒数据集Wine、小麦种子数据集seeds进行测试,本文从UCI官网上将这三个数据集下载下来,并放入和python文件同一个文件夹内即可。同时由于程序需要,将数据集的列的位置做出了略微改动。数据集具体信息如下表:
| 数据集 | 样本数 | 属性维度 | 类别个数 |
|---|---|---|---|
| Iris | 150 | 4 | 3 |
| Wine | 178 | 3 | 3 |
| Seeds | 210 | 7 | 3 |
数据集在我主页资源里有,免积分下载,如果无法下载,可以私信我。
1、Python3代码实现
import time
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from numpy import nonzero, array
from sklearn.cluster import KMeans
from sklearn.metrics import f1_score, accuracy_score, normalized_mutual_info_score, rand_score, adjusted_rand_score
from sklearn.preprocessing import LabelEncoder
from sklearn.decomposition import PCA
# 数据保存在.csv文件中
iris = pd.read_csv("dataset/Iris.csv", header=0) # 鸢尾花数据集 Iris class=3
wine = pd.read_csv("dataset/wine.csv") # 葡萄酒数据集 Wine class=3
seeds = pd.read_csv("dataset/seeds.csv") # 小麦种子数据集 seeds class=3
wdbc = pd.read_csv("dataset/wdbc.csv") # 威斯康星州乳腺癌数据集 Breast Cancer Wisconsin (Diagnostic) class=2
glass = pd.read_csv("dataset/glass.csv") # 玻璃辨识数据集 Glass Identification class=6
df = iris # 设置要读取的数据集
# print(df)
columns = list(df.columns) # 获取数据集的第一行,第一行通常为特征名,所以先取出
features = columns[:len(columns) - 1] # 数据集的特征名(去除了最后一列,因为最后一列存放的是标签,不是数据)
dataset = df[features] # 预处理之后的数据,去除掉了第一行的数据(因为其为特征名,如果数据第一行不是特征名,可跳过这一步)
attributes = len(df.columns) - 1 # 属性数量(数据集维度)
original_labels = list(df[columns[-1]]) # 原始标签
def initialize_centroids(data, k):
# 从数据集中随机选择k个点作为初始质心
centers = data[np.random.choice(data.shape[0], k, replace=False)]
return centers
def get_clusters(data, centroids):
# 计算数据点与质心之间的距离,并将数据点分配给最近的质心
distances = np.linalg.norm(data[:, np.newaxis] - centroids, axis=2)
cluster_labels = np.argmin(distances, axis=1)
return cluster_labels
def update_centroids(data, cluster_labels, k):
# 计算每个簇的新质心,即簇内数据点的均值
new_centroids = np.array([data[cluster_labels == i].mean(axis=0) for i in range(k)])
return new_centroids
def k_means(data, k, T, epsilon):
start = time.time() # 开始时间,计时
# 初始化质心
centroids = initialize_centroids(data, k)
t = 0
while t <= T:
# 分配簇
cluster_labels = get_clusters(data, centroids)
# 更新质心
new_centroids = update_centroids(data, cluster_labels, k)
# 检查收敛条件
if np.linalg.norm(new_centroids - centroids) < epsilon:
break
centroids = new_centroids
print("第", t, "次迭代")
t += 1
print("用时:{0}".format(time.time() - start))
return cluster_labels, centroids
# 计算聚类指标
def clustering_indicators(labels_true, labels_pred):
if type(labels_true[0]) != int:
labels_true = LabelEncoder().fit_transform(df[columns[len(columns) - 1]]) # 如果数据集的标签为文本类型,把文本标签转换为数字标签
f_measure = f1_score(labels_true, labels_pred, average='macro') # F值
accuracy = accuracy_score(labels_true, labels_pred) # ACC
normalized_mutual_information = normalized_mutual_info_score(labels_true, labels_pred) # NMI
rand_index = rand_score(labels_true, labels_pred) # RI
ARI = adjusted_rand_score(labels_true, labels_pred)
return f_measure, accuracy, normalized_mutual_information, rand_index, ARI
# 绘制聚类结果散点图
def draw_cluster(dataset, centers, labels):
center_array = array(centers)
if attributes > 2:
dataset = PCA(n_components=2).fit_transform(dataset) # 如果属性数量大于2,降维
center_array = PCA(n_components=2).fit_transform(center_array) # 如果属性数量大于2,降维
else:
dataset = array(dataset)
# 做散点图
label = array(labels)
plt.scatter(dataset[:, 0], dataset[:, 1], marker='o', c='black', s=7) # 原图
# plt.show()
colors = np.array(
["#FF0000", "#0000FF", "#00FF00", "#FFFF00", "#00FFFF", "#FF00FF", "#800000", "#008000", "#000080", "#808000",
"#800080", "#008080", "#444444", "#FFD700", "#008080"])
# 循换打印k个簇,每个簇使用不同的颜色
for i in range(k):
plt.scatter(dataset[nonzero(label == i), 0], dataset[nonzero(label == i), 1], c=colors[i], s=7, marker='o')
# plt.scatter(center_array[:, 0], center_array[:, 1], marker='x', color='m', s=30) # 聚类中心
plt.show()
if __name__ == "__main__":
k = 3 # 聚类簇数
T = 100 # 最大迭代数
n = len(dataset) # 样本数
epsilon = 1e-5
# 预测全部数据
labels, centers = k_means(np.array(dataset), k, T, epsilon)
# print(labels)
F_measure, ACC, NMI, RI, ARI = clustering_indicators(original_labels, labels) # 计算聚类指标
print("F_measure:", F_measure, "ACC:", ACC, "NMI", NMI, "RI", RI, "ARI", ARI)
# print(membership)
# print(centers)
# print(dataset)
draw_cluster(dataset, centers, labels=labels)
2、聚类结果分析
本文选择了F值(F-measure,FM)、准确率(Accuracy,ACC)、标准互信息(Normalized Mutual Information,NMI)和兰德指数(Rand Index,RI)作为评估指标,其值域为[0,1],取值越大说明聚类结果越符合预期。
F值结合了精度(Precision)与召回率(Recall)两种指标,它的值为精度与召回率的调和平均,其计算公式见公式:
P r e c i s i o n = T P T P + F P Precision=\frac{TP}{TP+FP} Precision=TP+FPTP
R e c a l l = T P T P + F N Recall=\frac{TP}{TP+FN} Recall=TP+FNTP
F − m e a s u r e = 2 R e c a l l × P r e c i s i o n R e c a l l + P r e c i s i o n F-measure=\frac{2Recall \times Precision}{Recall+Precision} F−measure=Recall+Precision2Recall×Precision
ACC是被正确分类的样本数与数据集总样本数的比值,计算公式如下:
A C C = T P + T N T P + T N + F P + F N ACC=\frac{TP+TN}{TP+TN+FP+FN} ACC=TP+TN+FP+FNTP+TN
其中,TP(True Positive)表示将正类预测为正类数的样本个数,TN (True Negative)表示将负类预测为负类数的样本个数,FP(False Positive)表示将负类预测为正类数误报的样本个数,FN(False Negative)表示将正类预测为负类数的样本个数。
NMI用于量化聚类结果和已知类别标签的匹配程度,相比于ACC,NMI的值不会受到族类标签排列的影响。计算公式如下:
N M I = I ( U , V ) H ( U ) H ( V ) NMI=\frac{I\left(U,V\right)}{\sqrt{H\left(U\right)H\left(V\right)}} NMI=H(U)H(V)I(U,V)
其中H(U)代表正确分类的熵,H(V)分别代表通过算法得到的结果的熵。
其具体实现代吗如下:
由于数据集中给定的正确标签可能为文本类型而不是数字标签,所以在计算前先判断数据集的标签是否为数字类型,如果不是,则转化为数字类型
def clustering_indicators(labels_true, labels_pred):
if type(labels_true[0]) != int:
labels_true = LabelEncoder().fit_transform(df[columns[len(columns) - 1]]) # 如果数据集的标签为文本类型,把文本标签转换为数字标签
f_measure = f1_score(labels_true, labels_pred, average='macro') # F值
accuracy = accuracy_score(labels_true, labels_pred) # ACC
normalized_mutual_information = normalized_mutual_info_score(labels_true, labels_pred) # NMI
rand_index = rand_score(labels_true, labels_pred) # RI
return f_measure, accuracy, normalized_mutual_information, rand_index
F_measure, ACC, NMI, RI = clustering_indicators(class_labels, label)
print("F_measure:", F_measure, "ACC:", ACC, "NMI", NMI, "RI", RI)
如果需要计算出聚类分析指标,只要将以上代码插入K-means实现代码中即可。
3、聚类结果
-
鸢尾花数据集Iris

Iris鸢尾花数据集原图

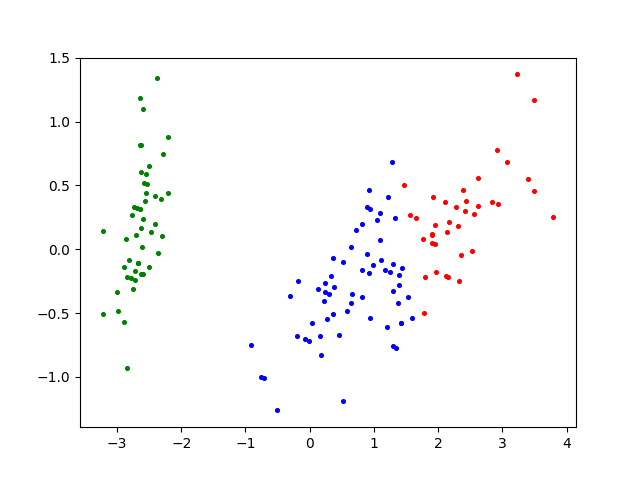
Iris鸢尾花数据集K-means聚类效果图 -
葡萄酒数据集Wine

Wine葡萄酒数据集原图

Wine葡萄酒数据集K-means聚类效果图 -
小麦种子数据集Seeds

Seeds小麦种子数据集原图

Seeds小麦种子数据集K-means聚类效果图
更多推荐
 已为社区贡献4条内容
已为社区贡献4条内容























所有评论(0)