github地址 https://github.com/HJCYFY/ECO.git

前一段时间将ECO_HC使用C++重新实现了一下，使用多线程速度上达到原matlab版的4倍左右，电脑上能达到100帧，某些情况下能达到160帧。如果你也准备实现，使用Eigen进行矩阵操作是个很好的选择。已经开源。

ECO的baseline是C-COT(Continuous Convolution Operator
Tracker),主要在一下三个方面有改进：
1.模型大小：高维特征(hog 31维，CN 10维)导致模型参数非常多，有时比输入图像的维度还要高，这样多的参数很容易导致Overfitting(过拟合)，提高了计算复杂度导致计算过慢。
2.训练集大小：传统的State-of-art方法需要大的训练集，由于他们的迭代优化算法。
3.模型更新：大多数DCF跟踪方法使用连续学习策略，每帧都更型模型，事实上这种更新可能造成跟踪效果下降。

C-COT原理简介

C-COT通过在连续域进行卷积实现了多分辨率特征的融合，这样我们就能灵活的选择Cell Size，通过连续方程直接获得目标得分亚网格上的位置。

C-COT有区别的从M个训练样本中学习一个卷积滤波器，与传统的DCF有别，每个特征维度有独立的解，特征通过一个插值模型转到连续域。

其中，$ X_d[n] $ 表示第n层特征，$ b_d $是周期T>0的插值核。最终得到$ J\lbrace x \rbrace$ 表示整个插值特征。
C-COT公式中一个连续多通道卷积滤波器被训练来预测目标得分

分数定义在对应的图像区域$ t\in [0,T) $,(2)中单通道T周期函数卷积定义为$ f*g(t) = 1/T \int_0^T f(t-\tau)g(\tau) ,{\rm d}\tau $,多通道定义为所有通道的和，滤波器的学习通过最小化下式：

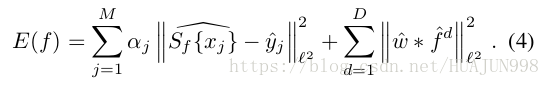样本$ x_j $的检测得分 $ y_j(t) $被设置为周期重复的高斯函数。通过L2归一化$ ||g||^2_{L2}=1/T\int_0^T |g(t)|^2 ,{\rm d}t $得到数据项加权分类误差,$ \alpha_j$是$ x_j $的权重大于0，正则化集成了空间惩罚$ w(t)$来缓解周期假设的缺点，同时允许扩展空间支持。在以前的DCF方法，，通过改变傅里叶基获得更易于处理的优化问题。Parseval公式意味着这里，$ \hat g$是T周期函数 $ g$ 的傅立叶序列系数 $ \hat g[k] = 1/T\int_0^Tg(t)e{-i\frac {2\pi}Tkt\rm }\rm dt$,$ \cal L^2$归一化定义为 $ ||\hat g||{L^2}2 = \sum{-\infty}^\infty |\hat g[k]|^2$,检测分数的傅立叶系数为$ \hat {S_f\lbrace x \rbrace} = \sum_{d=1}^D\hat f^dXd\hat b_d$ ,$ X^d $是$ x^d$的离散傅立叶变换。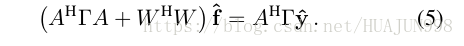实际上，我们假设滤波器$ f^d$拥有有限的非零傅立叶系数$ \lbrace\hat f^{d[k]\rbrace_{-K_d}}{K_d}$,$ K_d = \lfloor N_d/2 \rfloor$,等式（4）变成一个二次问题，通过解决归一化等式优化，这里，$ \hat f $和$ \hat y $是 $f_d$ 和$y_i$的傅立叶系数，$A$矩阵具有稀疏结构,对角块具有 $X_j^d[k]{\hat{b}}_d[k]$形式。$ \Gamma$是权重 $ \alpha _j$的对角矩阵，$ W$是卷积矩阵核为$\hat w[k]$ ,C-COT运用共轭梯度发迭代解决（5），因为它被证明有效地利用了问题的稀疏结构。
ECO

由于（3）式过多参数可能造成over-fitting，我们缓解这个问题通过引入分解卷积公式，这个策略减少深度特征80%参数，同时提高性能，此外，我们还提出了一个紧凑的样本分布的生成模型，这增强了多样性，避免了先前讨论的与存储大样本集相关的问题。最后我们解决模型更新问题。

我们首先介绍一个因式分解的卷积积分的方法，以减少模型中的参数的个数。我们观察到许多C-COT包含许多能量可以忽略不计的过滤器。他们对定位没有作用又耗费计算，我们用更小的基础滤波器代替每个特征通道一个独立的滤波器，那么d层特征的滤波器将是小滤波器的现行组合，新的多通道滤波器可以看多矩阵和向量的乘积，我们得到分解的卷积操作

$f$是分解的滤波器，$P$是对应每个通道的矩阵，分解卷积可分为两步，特征向量$ J\lbrace X\rbrace(t) $首先和$ P^T$相乘，得到的特征与滤波器做卷积。矩阵$ P^T$像一个线性的缩减为度的操作，通过最小化分解操作（6）的分类误差（3），我们联合学习的滤光器F和矩阵P。最终，通过线性化残差，我们使用高斯牛顿迭代方法求解。

我们分解卷积运算的主要目的是减少计算的复杂性和内存。由于滤波器的适应性，可以从第一帧学习矩阵P。这有两个重要的含义。首先，只有投影的特征映射需要存储，从而导致显著的内存节省。第二，滤波器可以在后续的帧中使用投影的特征图作为输入进行更新。这降低了特征维数D到维度C。

我们提出了一个紧凑的样本集，避免了先前所讨论的存储大量样本的问题。大多数DCF跟踪程序，在每一帧j添加样本$ X_j$,权重通常设置为指数衰减，由学习率$\gamma$控制。如果样本数量达到最大限制权重最小的样本被代替，然而，这种策略需要一个大样本m来获得一个有代表性的样本集。我们观察到，在每一帧中收集新的样本会导致样本集大量冗余，我们使用样本集的概率生成模型，通过消除冗余和增强多样性来实现对样本的紧凑描述。

ECO的方法是基于样本特征映射x和相应的期望输出分数y的联合概率分布p（x，y），给定p（x，y），直观的目标是找到最小化期望相关误差的滤波器。这是通过替换（3）

我们发现期望的样本x的输出y的形状是注定的，这里是一个高斯函数，在（3）中的标签函数$y_i$只与将峰值与目标中心相匹配的转换不同,这种对准通过移动特征图x来执行。

更新GMM，给定一个新的样本$X_j$,我们首先初始化一个新的对象m，其中${\pi }_m=\gamma ,{\mu }_m=x_j$ ,如果对想得数量超过了限制L，我们简化GMM，舍弃一个权重${\pi }_m$小于阈值的对象，否则我们将最近的对象k和l组成一个共同的对象n，

在傅里叶域使用的Parseval公式快速计算比较距离$ ||\mu _k−\mu_l||$。

最终我们期望的Loss （10）近似位

注意，高斯均值$ \mu _l$ 和优先级权重 $ \pi$直接代替（3）中的$x_j$和$\alpha _j$,我们可以用之前的策略。与（3）关键的不同是样本的数量从M减少到L，L根据经验可以被设置为M/8，获得跟踪性能的极大提高。

基于DCF跟踪的标准方法是在每个帧中更新模型。在c-cot，这意味着优化（3）后，每增加一个新的样本，通过迭代求解方程（5）。基于迭代优化的DCF方法的损失函数在帧间逐渐变化。因此，滤波器的当前估计提供了迭代搜索的良好初始化。然而，更新每个帧中的滤波器对计算能力有严重的影响。

我们用稀疏更新策略代替连续更新，直观地说，只有在目标发生充分变化时，才能开始优化过程。然而，找到这样的条件是不容易的，可能会导致不必要的复杂的尝试。此外优化条件与损失（3）的梯度有关，非常耗费计算，因此我们N帧更新一次滤波器。