目录

一、简介

二、原理及代码

1、数据准备

2、构造神经网络

3、Python代码实现（训练-效果）

参考

---

一、简介

        PyTorch是一个开源的Python机器学习库，基于Torch，用于自然语言处理等应用程序。2017年1月，由Facebook人工智能研究院（FAIR）基于Torch推出了PyTorch。它是一个基于Python的可续计算包，提供两个高级功能：1、具有强大的GPU加速的张量计算（如NumPy）。2、包含自动求导系统的深度神经网络[1]。

二、原理及代码

1、数据准备

        我们用美国国家标准与技术研究所的数据集-MNIST。这个数据集有两部分：训练集和测试集，顾名思义训练集是用来训练神经网络的，测试集是用来测试神经网络训练后的效果。训练集由250个人手写的数字构成，其中50%是高中学生，50%是人口普查的工作人员。测试数据集也是同样比例的手写数字。这些图片都是28X28灰度像素的。如：

下载

import torchvision.datasets as dsets

#MNIST dataset
train_dataset = dsets.MNIST(root='/ml/pymnist',  #选择数据的根目录
                            train=True,#选择训练集
                            transform=None,#不考虑使用数据预处理
                            download=True #是否从网络上下载图片
)

test_dataset = dsets.MNIST(root='/ml/pymnist',#选择数据的根目录
                           train=False,#选择测试集
                           transform=None,#不考虑使用任何数据预处理
                           download=True #是否从网络上下载图片
)

查看数据​​​​​​​

x_train=train_dataset.train_data.numpy().reshape(-1,28*28)  #将6万张28X28的图片，转换为一维数组
#print(x_train.shape)  #输出;(60000, 784)  

imgIndex = 22

#取其中的一个图片
x1 = x_train[imgIndex].reshape(28,28)  #将一维数组转换为二阶矩阵 28X28，还原图片矩阵
#print(x1)  #输出28X28二维矩阵


y_train = train_dataset.train_labels.numpy()  #转换为numpy数据
#print(y_train.shape) #输出torch.Size([60000]) ，有60000张图片的标签，正好与上面图片数量对应

y1 = y_train[imgIndex]
#print(y1)  #输出：5

#图片显示
import matplotlib.pyplot as plt
plt.imshow(x1,cmap=plt.cm.binary)  #显示图片设置
plt.title("number:" + str(y1))
plt.show()

2、构造神经网络

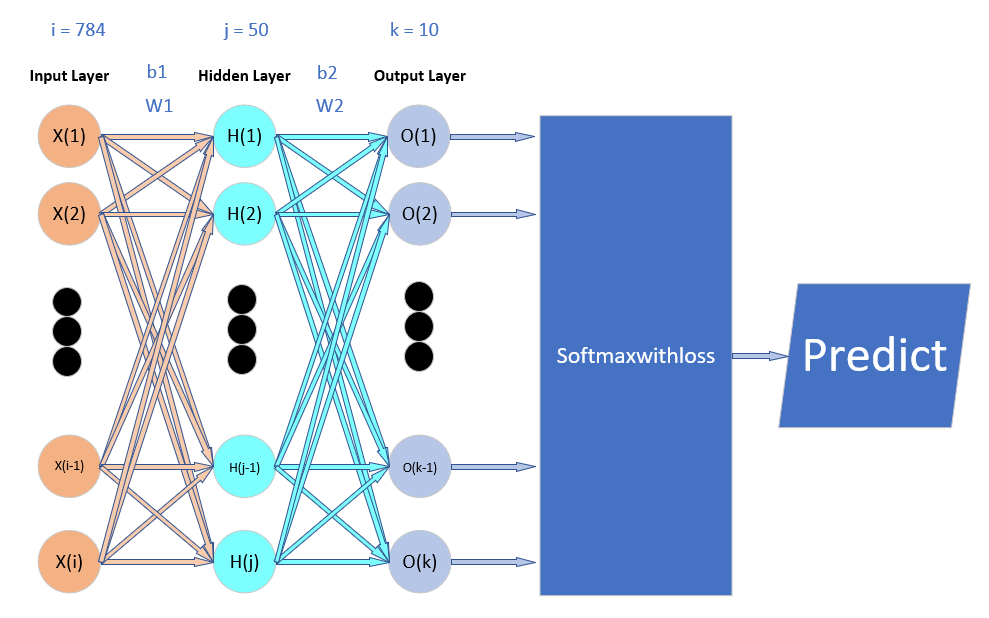
        从上述的数据集我们知道一个图片有28X28 = 784个像素，因此，输入层有784个神经元。隐藏层的神经元可以自定义，这里就设置50个。输出层的神经元个数和数据集元素的类别有关，因为数据集中的数字只有0~9，即只有10种类别，因此，我们将输出层的神经元个数设置为10个。激活函数选择现在比较流行的ReLU函数：

图 ReLU函数图

        ReLU函数的特点是：在程序中计算快（因为不需要计算指数）；在输入为正数的时候不存在梯度饱和问题。 

图 神经元连接

图 神经网络层

        Affine表示将输入进行加权求和，然后传给激活函数ReLU，也可以认为是隐藏层的子层。

在输出层中加入了Softmaxwithloss层处理误差。由于Softmaxwithloss层之前没提到，现在介绍一下。

先选择损失函数：

y：输出神经元的真实值

p：输出神经元的预测值

C：输出神经元的个数

其中y是经过编码变为one-hot code，即y中的元素只能有一个是1，其他为0， 这样输出神经元每输出一次，我们就可以告诉它那个输出神经元输出的是正确值。   详细可参考

独热码 - 搜狗百科独热码，在英文文献中称做 one-hot code, 直观来说就是有多少个状态就有多少比特，而且只有一个比特为1，其他全为0的一种码制。通常，在通信网络协议栈中，使用八位或者十六位状态的独热码，且系统占用其中一个状态码，余下的可以供用户使用。例如，有6个状态的独热码状态编码为：000001，000010，000100，001000，010000，100000。再如，有十六个状态的独热码状态编码应https://baike.sogou.com/v68067077.htm?fromTitle=%E7%8B%AC%E7%83%AD%E7%A0%8现假设ReLU2输出数据为z，经过softmax函数输出预测值pi：

将预测值代入损失函数L即可求出误差。

3、Python代码实现（训练-效果）

from collections import OrderedDict

import numpy as np

import torch
from torch.utils.data import DataLoader
import torchvision.datasets as dsets
import torchvision.transforms as transforms

import numpy as np

batch_size = 100
#MNIST dataset
train_dataset = dsets.MNIST(root='/ml/pymnist',  #选择数据的根目录
                            train=True,#选择训练集
                            transform=None,#不考虑使用数据预处理
                            download=False #是否从网络上下载图片，第一次要选True
)

test_dataset = dsets.MNIST(root='/ml/pymnist',#选择数据的根目录
                           train=False,#选择测试集
                           transform=None,#不考虑使用任何数据预处理
                           download=False#是否从网络上下载图片，第一次要选True
)

x_train=train_dataset.train_data.numpy().reshape(-1,28*28)
y_train_tmp=train_dataset.train_labels.reshape(train_dataset.train_labels.shape[0],1)
y_train=torch.zeros(y_train_tmp.shape[0],10).scatter_(1,y_train_tmp,1).numpy()
#print(y_train)

x_test = test_dataset.test_data.numpy().reshape(-1,28*28)
y_test_tmp = test_dataset.test_labels.reshape(test_dataset.test_labels.shape[0],1)
y_test = torch.zeros(y_test_tmp.shape[0],10).scatter_(1,y_test_tmp,1).numpy()

class Relu:
    def __init__(self):
        self.x=None
        return
    def forward(self,x):
        self.x=np.maximum(0,x)
        out=self.x
        return out
    def backward(self,dout):
        dx=dout
        dx[self.x<=0]=0
        #print("dout:",dx)
        return dx


class Affine:
    def __init__(self,W,b):
        self.W=W
        self.b=b
        self.x=None
        self.dW=None
        self.db=None
        return
    def forward(self,x):
        self.x=x
        out=np.dot(x,self.W)+self.b
        return out
    def backward(self,dout):
        dx=np.dot(dout,self.W.T)
        self.dW=np.dot(self.x.T,dout)
        self.db=np.sum(dout,axis=0)
        #print("db:",self.db)
        return dx

class SoftmaxWithLoss:
    def __init__(self):
        self.loss=None #损失
        self.p=None #softmax输出
        self.y=None #监督数据代表真值，one-hot vector
        return
    def softmax(self,x):
        if x.ndim==2:  #ndim返回的是数组的维度，返回的只有一个数，该数即表示数组的维度。
            c=np.max(x,axis=1)
            x=x.T-c #溢出决策
            y=np.exp(x)/np.sum(np.exp(x),axis=0)
            return y.T
        c=np.max(x)
        exp_x = np.exp(x-c)
        return exp_x/np.sum(exp_x)
    def cross_entropy_error(self,p,y):
        delta=1e-7
        batch_size=p.shape[0]
        return -np.sum(y*np.log(p+delta))/batch_size

    def forward(self,x,y):
        self.y=y
#         print("self.y",self.y)
        self.p=self.softmax(x)
        self.loss=self.cross_entropy_error(self.p,self.y)
        #print(self.loss)
        return self.loss
    def backward(self,dout=1):
        batch_size=self.y.shape[0]
        dx=(self.p-self.y)/batch_size  #设置预测了一小批数据获取的误差
#         print(dx.shape) #(100, 10)
        return dx

class TwoLayerNet:

    def __init__(self,input_size,hidden_size,output_size,weight_init_std=0.01):
        #初始化权重
        self.params={}
        self.params['W1']=weight_init_std*np.random.randn(input_size,hidden_size)   #隐藏层的权重
#         print(self.params['W1'])

        self.params['b1']=np.zeros(hidden_size)  #隐藏层的偏置值
        self.params['W2']=weight_init_std*np.random.randn(hidden_size,output_size) #输出层的权重
        self.params['b2']=np.zeros(output_size)  #输出层的偏置值

        #生成神经网络层
        self.layers=OrderedDict() #有序字典;基本的dict无法保证顺序，keys映射为哈希值，而此值不是按照顺序存储在散列表中的。所以遇到要确保字典keys有序场景，就要使用OrderedDict.
        self.layers['Affine1']=Affine(self.params['W1'],self.params['b1'])  #生成隐藏层的神经元
        self.layers['Relu1']=Relu()  #生成隐藏层的激活函数 
        self.layers['Affine2']=Affine(self.params['W2'],self.params['b2'])  #生成输出层的神经元
        self.layers['Relu2']=Relu()  #生成输出层的激活函数 
        self.lastLayer = SoftmaxWithLoss()   

        return

    def predict(self,x):
        for layer in self.layers.values(): #每层都前向传播
            x=layer.forward(x)
        return x

    #x：输入数据，y：监督数据
    def loss(self,x,y):
        p=self.predict(x)  #预测了一次
        return self.lastLayer.forward(p,y)  #最后一层做了一次前向传播
    
    def accuracy(self,x,y):
        #预测一下
        p=self.predict(x) 
        #print("p:",p.shape)  #p: (10000, 10)
        p=np.argmax(p,axis=1) #argmax返回某一列的最大值的下标
        #print("p:",p.shape)  #p: (10000,)
        y=np.argmax(y,axis=1)

        accuracy=np.sum(p==y)/float(x.shape[0])  #预测所有数据，看看能有多少个正确
        return accuracy

    """
    实现梯度，但是没有修改权值
    """
    def gradient(self,x,y):
        #forward
        self.loss(x,y)  

        #backward
        dout=1
        dout=self.lastLayer.backward(dout) #(100, 10) #一批数据的误差
#         print("dout:",dout)  #各个输出神经元的误差

        layers=list(self.layers.values())
        #print("layers:",layers)
        layers.reverse()  #反转
        for layer in layers:
            dout=layer.backward(dout)  #此处实现逐层向前传播，ReLU2 -》 Affine2 -》ReLU1 -》Affine1
#             print("dout:",dout)

        #设定
        grads={}
        grads['W1'],grads['b1']=self.layers['Affine1'].dW,self.layers['Affine1'].db
        grads['W2'],grads['b2']=self.layers['Affine2'].dW,self.layers['Affine2'].db
        
        return grads

train_size = x_train.shape[0] 
iters_num = 600
learning_rate = 0.001
epoch = 5
batch_size = 100

network = TwoLayerNet(input_size = 784,hidden_size = 50,output_size = 10)

#训练，分批训练：即将总数分为epoch批，训练完一批后再进行下一批训练
    #注意训练不会永久保存权值
for i in range(epoch): #分批训练
    print("current epoch is：", i)
    for num in range(iters_num):
        batch_mask = np.random.choice(train_size,batch_size)  #>>> np.random.choice(5, 3)   输出array([0, 3, 4]) # random
                                                                #在train_size范围内随机选batch_size个数，形成一维数组
        #print(batch_mask)
        x_batch = x_train[batch_mask]  #在总数据中选一小批
        #print(x_batch.shape)
        y_batch = y_train[batch_mask]

##########################梯度下降法####################################
        grad = network.gradient(x_batch,y_batch)
       #print("grad",grad)

        for key in ('W1','b1','W2','b2'):
            network.params[key] -= learning_rate*grad[key]  #实现梯度下降学习
############################################################################
        loss = network.loss(x_batch,y_batch)  # 计算损失值
        if num % 100 ==0:
            print("loss: ",loss)
#print(x_test.shape,y_test.shape)
print('准确率：',network.accuracy(x_test,y_test)*100,'%')  #将10000张图片让其识别，看看正确率



"""
我们随机选一张图片让其识别
"""
x_train=train_dataset.train_data.numpy().reshape(-1,28*28)  #将6万张28X28的图片，转换为一维数组
#print(x_train.shape)  #输出;(60000, 784)  

import random
imgIndex = random.randint(0,x_train.shape[0]) #在60000张图片中任选一张

#取其中的一个图片
x1 = x_train[imgIndex].reshape(28,28)  #将一维数组转换为二阶矩阵 28X28，还原图片矩阵
#print(x1)  #输出28X28二维矩阵

p = network.predict(x1.reshape(-1,28*28))
p = np.argmax(p,axis=1)
# print("预测：",p)

y_train = train_dataset.train_labels.numpy()  #转换为numpy数据
#print(y_train.shape) #输出torch.Size([60000]) ，有60000张图片的标签，正好与上面图片数量对应

y1 = y_train[imgIndex]
#print(y1)  #输出：5

#图片显示
import matplotlib.pyplot as plt
plt.imshow(x1,cmap=plt.cm.binary)  #显示图片设置
plt.title("predicted number:" + str(y1))
plt.show()

训练过程损失函数输出

current epoch is：0
loss:  2.266151231985748
loss:  0.3724026421914155
loss:  0.19832547560691383
loss:  0.22490945327141837
loss:  0.1661208009051106
loss:  0.258948805644127
current epoch is：1
loss:  0.13390206665995094
loss:  0.1320481015568629
loss:  0.07788363928512003
loss:  0.19471398981094826
loss:  0.06045146962828367
loss:  0.22834023219954858
current epoch is：2
loss:  0.08998278435494232
loss:  0.13953232891168038
loss:  0.05586382405036148
loss:  0.058314648911912174
loss:  0.09738683049424073
loss:  0.05205461861693841
current epoch is：3
loss:  0.045705761642539054
loss:  0.12238526156163801
loss:  0.07323083292990847
loss:  0.0800588072480463
loss:  0.06406958008082181
loss:  0.09598045459144477
current epoch is：4
loss:  0.08828214574587279
loss:  0.15144249360478873
loss:  0.08583687343851693
loss:  0.09221907715731381
loss:  0.03905677555959257
loss:  0.0632881118798391
准确率：96.23 %

        最后预测正确。

参考

【1】PyTorch_百度百科

【2】《深度学习与图像识别原理与实践》 魏溪含等著